Introduction

Dans ce document, nous allons implémenter différents algorithmes d’isomorphismes de sous graphes, optimaux ou non.

Dans un premier temps, nous allons nous concentrer sur 3 algorithmes différents, à savoir :

Création des graphes

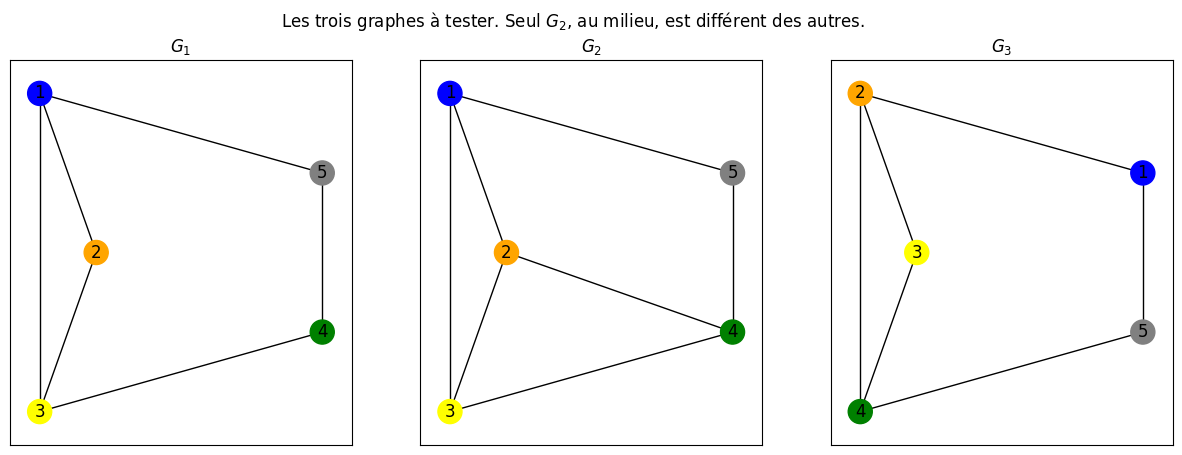
Avant d’implémenter les algos, nous allons créer 3 graphes simples à visualiser. Deux d’entre eux ($G_1$ et $G_3$) sont isormorphes. C’est à dire qu’ils représentent le même graphe, mais que l’ordre des noeuds de chacun des graphes est différent. Il y a une permutation des nœuds.

$G_2$ n’est pas isomorphe à $G_1$ et $G_3$

import networkx as nx
import matplotlib.pyplot as plt

G1 = nx.Graph([[1,2],[2,3],[3,4],[4,5],[5,1],[1,3]])
colors = ["orange","yellow","green","grey","blue"]
pos1 = {1:(0,4), 2:(.2,2),3:(0,0),4:(1,1),5:(1,3)}
for n in G1.nodes():
    G1.nodes[n]["label"] = 1

G2 = nx.Graph([[1,2],[2,3],[3,4],[4,5],[5,1],[1,3],[2,4]])
colors = ["orange","yellow","green","grey","blue"]
pos1 = {1:(0,4), 2:(.2,2),3:(0,0),4:(1,1),5:(1,3)}
for n in G2.nodes():
    G2.nodes[n]["label"] = 1

# G1 and G3 are isomorphic
G3 = nx.Graph([[1,2],[2,3],[3,4],[4,5],[5,1],[2,4]])
colors = ["blue","orange","yellow","green","grey"]
pos2 = {1:(1,3),2:(0,4), 3:(.2,2),4:(0,0),5:(1,1)}
for n in G3.nodes():
    G3.nodes[n]["label"] = 1

fig,axes = plt.subplots(1,3,figsize=(15,5))
nx.draw_networkx(G1,pos=pos1,node_color=colors,ax=axes[0])
nx.draw_networkx(G2,pos=pos1,node_color=colors,ax=axes[1])
nx.draw_networkx(G3,pos=pos2,node_color=colors,ax=axes[2])
for i in range(3):
    axes[i].set_title(f"$G_{i+1}$")
fig.suptitle("Les trois graphes à tester. Seul $G_2$, au milieu, est différent des autres.");

Weisfeler - Lehman

Le WL test est un test d’isomorphisme itératif non optimal. C’est à dire que le résultat de l’algorithme n’est pas tout le temps exact au regard de la relation d’isomorphisme entre deux graphes. Si le résultat du test est que les deux graphes sont non isomorphes, alors les deux graphes seront réellement différents. À l’inverse, si le résultat indique que les deux graphes sont isomorphes, le résultat peut être faux pour certains cas particuliers. Ce désavantage est contre balancé par la complexité polynomiale de l’algorithme.

Quelques ressources:

De manière générale, l’algorithme consiste à calculer une signature du graphe à partir de signatures de chacun des noeuds, chaque signature prenant en compte le voisinage des noeuds. Si l’ensemble des signatures des noeuds des deux graphes sont équivalentes, alors on conclura à un isomorphisme entre les graphes.

Notes

L’algo étape par étape

Caractériser le voisinage

La première étape de l’algo consiste à agréger l’information concernant le voisinage de chacun des noeuds. Par exemple pour le noeud 1 de $G_1$ :

G_test = G1.copy()
labels = dict(G_test.nodes(data="label"))
labels_neighbors = [labels[m] for m in G_test[1]]
labels_neighbors.sort()
print(labels_neighbors)

[1, 1, 1]

Ensuite, les étiquettes des voisins est agrégé avec l’étiquette du noeud courant afin de caractériser la structure locale autour de chaque noeud. Un ‘hash’ est calculé afin d’identifier simplement les environnements similaires.

new_label = [labels[1]] + labels_neighbors
new_desc = hash(tuple(new_label)) # hash sur immutable
G_test.nodes[1]["label"]=new_desc # mise à jour du label
print(G_test.nodes[1]["label"])
print(labels)

-84722638022233667
{1: 1, 2: 1, 3: 1, 4: 1, 5: 1}

Partionnement des nœuds

Une fois l’étape précédente effectuée pour chaque noeud, chaque noeud a un nouveau label caractérisant son voisinage proche. On peut alors calculer une description du graphe en calculant l’histogramme des nouveaux labels. Cela indiquera combien de noeuds ont un voisinage similaire, et cette opération n’est pas sensible aux permutations choisies pour parcourir les noeuds du graphe.

for n in range(2,6): #on met à jour les autres noeuds
    print(f"Mise à jour noeud {n}")
    labels_neighbors = [labels[m] for m in G_test[n]]
    labels_neighbors.sort()
    new_label = [labels[n]] + labels_neighbors
    print(new_label)
    new_desc = hash(tuple(new_label)) # hash sur immutable
    G_test.nodes[n]["label"]=new_desc # mise à jour du label
    print(G_test.nodes[n]["label"])

Mise à jour noeud 2
[1, 1, 1]
5750192569890809213
Mise à jour noeud 3
[1, 1, 1, 1]
-84722638022233667
Mise à jour noeud 4
[1, 1, 1]
5750192569890809213
Mise à jour noeud 5
[1, 1, 1]
5750192569890809213

def compute_wl_label(graph):
    labels = {}
    for n in graph.nodes():
        label = graph.nodes[n]["label"]
        if label in labels:
            labels[label].append(n)
        else:
            labels[label] = [n]
    return labels

labels = compute_wl_label(G_test)
print(labels)

{-84722638022233667: [1, 3], 5750192569890809213: [2, 4, 5]}

Ici, on observe que le noeud 2,4 et 5 ont un même label, alors que 1 et 3 ont un label différent. Puisque dans notre cas tous les labels sont égaux, nous avons simplement discriminé sur le degré de chacun des noeuds.

Itérations

Afin de prendre en compte un voisinage de plus en plus grand, les deux étapes précédentes sont répétées jusqu’à que l’une des deux conditions suivantes soient rencontrées :

#Second itération
labels = dict(G_test.nodes(data="label"))
for n in G_test.nodes(): #on met à jour les autres noeuds
    print(f"Mise à jour noeud {n}")
    labels_neighbors = [labels[m] for m in G_test[n]]
    labels_neighbors.sort()
    new_label = [labels[n]] + labels_neighbors
    print(new_label)
    new_desc = hash(tuple(new_label)) # hash sur immutable
    G_test.nodes[n]["label"]=new_desc # mise à jour du label
    print(G_test.nodes[n]["label"])

labels = compute_wl_label(G_test)
print(labels)

Mise à jour noeud 1
[-84722638022233667, -84722638022233667, 5750192569890809213, 5750192569890809213]
-7481653653512719100
Mise à jour noeud 2
[5750192569890809213, -84722638022233667, -84722638022233667]
1651756523991284482
Mise à jour noeud 3
[-84722638022233667, -84722638022233667, 5750192569890809213, 5750192569890809213]
-7481653653512719100
Mise à jour noeud 4
[5750192569890809213, -84722638022233667, 5750192569890809213]
-224185658846573216
Mise à jour noeud 5
[5750192569890809213, -84722638022233667, 5750192569890809213]
-224185658846573216
{-7481653653512719100: [1, 3], 1651756523991284482: [2], -224185658846573216: [4, 5]}

Au bout de la deuxième itération, on observe que la partition 2,4,5 a été splitté en deux : 2 et 4,5. Donc on continue !

Conclusion du test d’isomorphisme

Lorsque nous allons appliquer l’algorithme itératif décrit plus haut à chacun des deux graphes à comparer, nous obtenons une partition pour chacun des graphes. La conclusion du test d’isomophisme est déduite de la comparaison des histogrammes de chacune des partitions. Si les deux graphes ont le même nombre de noeuds avec un label similaires, alors nos deux graphes sont potentiellement isomorphes. À l’inverse, si les histogrammes sont différents, alors nous pouvons conclure avec certitude que les deux graphes sont isomorphes.

# Calcul de l'histogramme des labels de G_test
histogramme = {label : len(labels[label]) for label in labels}
print(histogramme)

{-7481653653512719100: 2, 1651756523991284482: 1, -224185658846573216: 2}

Version finale du code

def wl_test_id(graph):
    LABEL_WL = 'wl'
    """
    Returns a dictionnary labels LABEL_WL as keys and list of nodes having this label as value iterative wl
    """
    def compute_wl_label(graph):
        labels = {}
        for n in graph.nodes():
            label = graph.nodes[n][LABEL_WL]
            if label in labels:
                labels[label].append(n)
            else:
                labels[label] = [n]
        return labels

    def compute_wl_signature(graph):
        """
        Compute an histogram from the dicts of labels. 
        """
        labels = compute_wl_label(graph)
        return {label : len(labels[label]) for label in labels}

    def compute_partition(graph):
        """
        Returns a list where each element is a list of nodes having the same label 
        """
        labels = compute_wl_label(graph)
        partition = list(labels.values())
        [l.sort() for l in partition]
        partition.sort()
        return partition

    iter = 0
    old_partition = {}
    conv = False
    # Initialisation des labels
    for n in graph.nodes():
        graph.nodes[n][LABEL_WL] = graph.nodes[n]["label"]

    # max number of iterations is the number of nodes
    while (iter <  graph.order() and not conv):
        #compute tuple
        old_labels = dict(graph.nodes(data=LABEL_WL))
        for n in graph.nodes():
            # we compute the new label
            labels_neighbors = [old_labels[m] for m in graph[n]]
            labels_neighbors.sort()
            # compute hash
            new_label_list = [old_labels[n]] + labels_neighbors
            new_desc = hash(tuple(new_label_list)) # hash sur immutable
            graph.nodes[n][LABEL_WL]=new_desc
        # partitions
        partition = compute_partition(graph)
        if partition == old_partition:
            conv = True
        old_partition=partition
        iter += 1
    return compute_wl_signature(graph)

def wl_test(graph_1,graph_2):
    return wl_test_id(graph_1) == wl_test_id(graph_2)

print(f"$G_1$ $G_3$ sont isomorphes : {wl_test(G1,G3)}")
print(f"$G_1$ $G_1$ sont isomorphes : {wl_test(G1,G1)}")
print(f"$G_1$ $G_2$ sont isomorphes : {wl_test(G1,G2)}")

$G_1$ $G_3$ sont isomorphes : True
$G_1$ $G_1$ sont isomorphes : True
$G_1$ $G_2$ sont isomorphes : False

Conclusion

Ce test d’isomorphisme, rapide à implémenter et à comprendre a été remis au gout du jour par les noyaux sur graphes (Weisfeler Lehman Graph kernel) ainsi que par l’étude théorique de la capacité des Graph Neural Networks à distinguer deux graphes différents.